


A machine learning project exploring tree-based models for poker hand classification, featuring build-from-scratch model, custom preprocessing, and model optimisation.
View on GitHub





This project explores tree-based machine learning models for poker hand classification, including a custom-built decision tree. It highlights the importance of feature engineering in enhancing model accuracy for complex tasks.
The project involved three pre-built models and one custom-built model:
The dataset used in this project is the Poker Hand dataset from the UCI Machine Learning Repository. The dataset contains 1,025,010 instances (25,010 for train and 1,000,000 for test), each representing a poker hand with 10 attributes (5 cards with rank and suit). The goal is to predict the poker hand rank based on these attributes into 10 classes of from 0 (Nothing) to 9 (Royal Flush).
The project explores different preprocessing techniques to improve model performance, including:
Basic card rank and suit representation
Added card frequency counts and sequential checks
Incorporated flush detection and card pattern analysis
Added highest and second-highest card count metrics
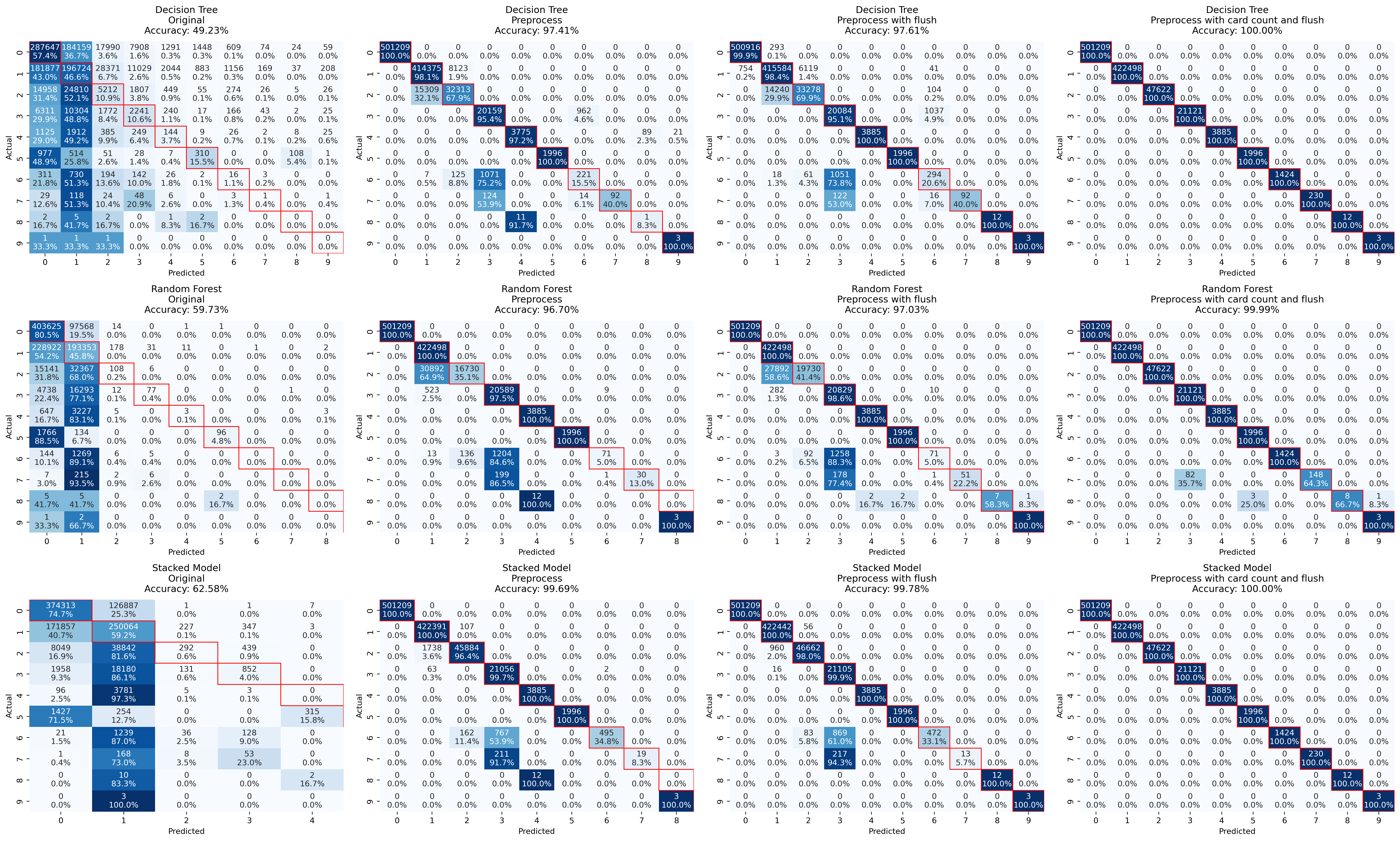
Confusion Matrix Results
It is seen that the models struggled to distinguish between poker hands using raw features like suits and ranks directly. This is expected, as raw numerical or categorical data often lacks the necessary abstraction for models to understand complex relationships in the data.
Introducing counts of cards by rank and suit, as well as checks for sequential cards, appears to have improved accuracy significantly (from 49-62% to 96-99%). This aligns with the principle that good feature engineering can help models better capture domain-specific relationships, in this case, identifying pairs or straights.
However, models are still struggling with hands that share overlapping characteristics (Straight and Flush versus Straight Flush, Three of a kind versus Four of a kind versus Full House, or even Royal Flush).
With Flush problem, a logical solution is to add a feature that specifically determines if a hand is a Flush. This will likely resolve ambiguity for Flush-related hands, including Straight Flush and Royal Flush.
Finally, the addition of features for the highest and second-highest card counts seems to have addressed ambiguities among Three of a Kind, Four of a Kind, and Full House.
There can be other alternatives in dealing with imbalanced dataset, such as oversampling and undersampling. However, for a game of poker where rules are well-defined, a meticulous feature engineering process seems easier and can lead to perfect classification results.
Thanks to the internet and the guide from GenAI, I was, once again, be able to understand the concept of Decision Tree and implement it from scratch. What makes decision trees particularly interesting is that while their mathematical foundation is relatively straightforward (mainly information theory and probability), the implementation challenges lie in:
Building a decision tree from scratch provided greater in-depth into both the simplicity and complexity of tree-based models. While the mathematical concepts might be straightforward, the implementation details and optimisation considerations is what makes it worthwhile. The final tree structure efficiently captured poker hand patterns:
Root (max_card_count = 1)
├── No Repeats Branch
│ ├── Check Sequential
│ │ ├── Check Flush → Royal/Straight Flush
│ │ └── No Flush → Straight
│ └── Not Sequential
│ ├── Check Flush → Flush
│ └── No Flush → Nothing
└── Has Repeats Branch
├── Second Count = 1
│ └── Check Max Count → One Pair/Three of Kind/Four of Kind
└── Second Count = 2
└── Check Max Count → Two Pairs/Full House
I wrote more about how I built the custom model in the GitHub repository, so feel free to check it out.
To my knowledge in the past about decision trees, I thought they were simple models that could be easily understood and implemented, especially compared to Random Forests. And it is indeed that way on concept level, but the implementation details can be quite complex. If easy, Linear Regression might be considered the simplest in terms of both concept and implementation, as it involves straightforward matrix operations and gradient descent. Neural networks, while more complex in architecture, can actually be simpler to implement from scratch than decision trees because their building blocks (forward pass, backward pass, gradient descent) are more linear in nature.
For Random Forests, the complexity lies in the ensemble nature of the model, where multiple decision trees are combined. While it is easy to imagine a Random Forest is indeed a collection (or "forest") of decision trees, its structure and operation can be quite hard to grasp since you need to wrap the base DT algorithm within additional infrastructure. But that is the talk for another day.
For the full code and documentation, visit the GitHub repository.